PCA: Principal Component Analysis

Andrew Irwin, a.irwin@dal.ca

2024-03-06

Plan

  • What is PCA and why do we use it?

  • Demonstration with gapminder data in 3 dimensions

  • More demonstrations

What is PCA?

  • A tool for simplifying data sets with many variables down to a small number

  • Works best with quantitative variables that are partially correlated

  • Can be used with one or more categorical variables to identify subgroups

  • Main results are

    • Spatial pattern of points (with categorical labels)
    • Directions of principal components along original axes (loadings)
    • Amount of variation along each PC axis

  • Be careful with scaling and units

Example data

Interactive version

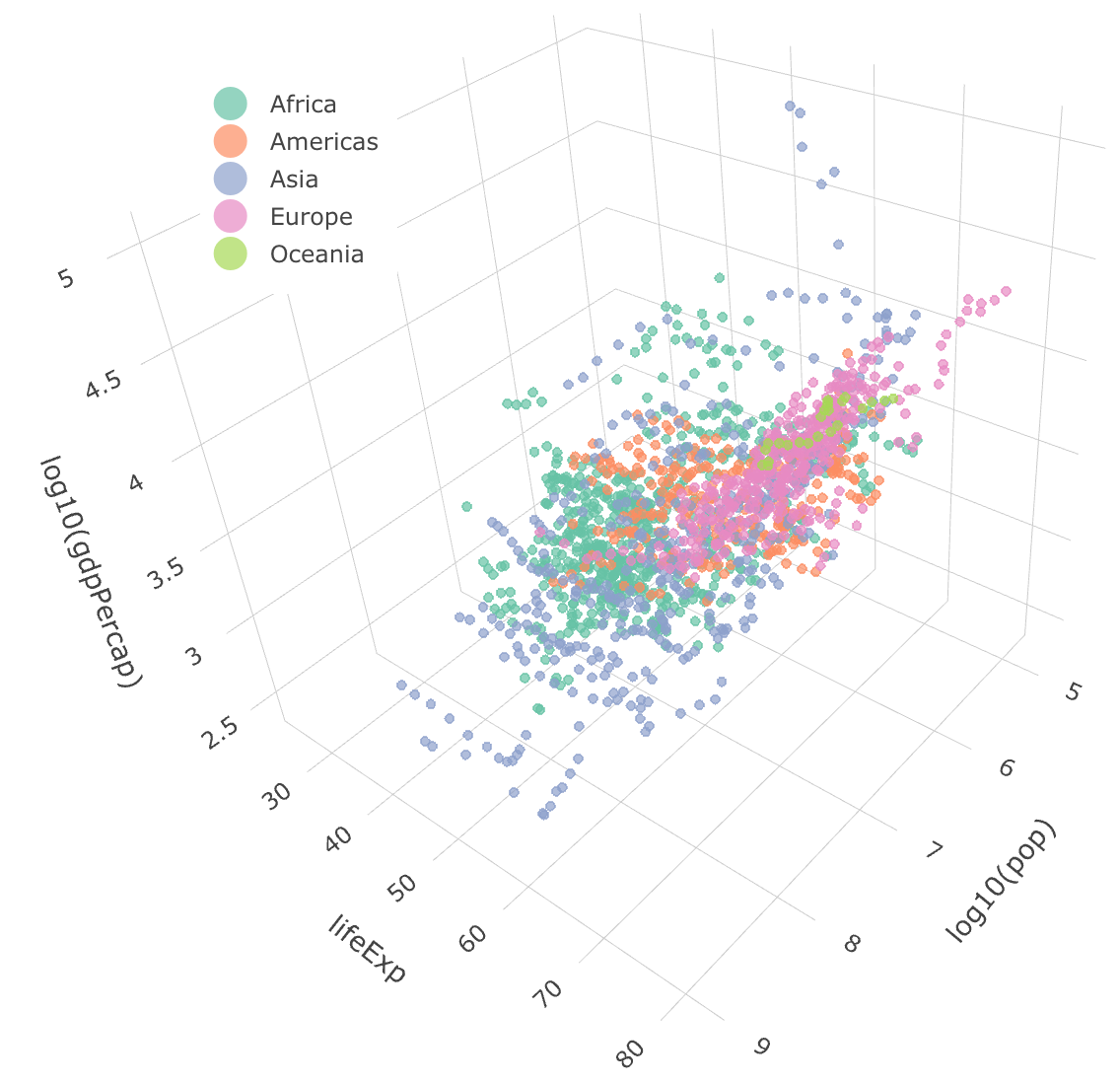
Plot made with plot_ly function in plotly package.

Pairs plot

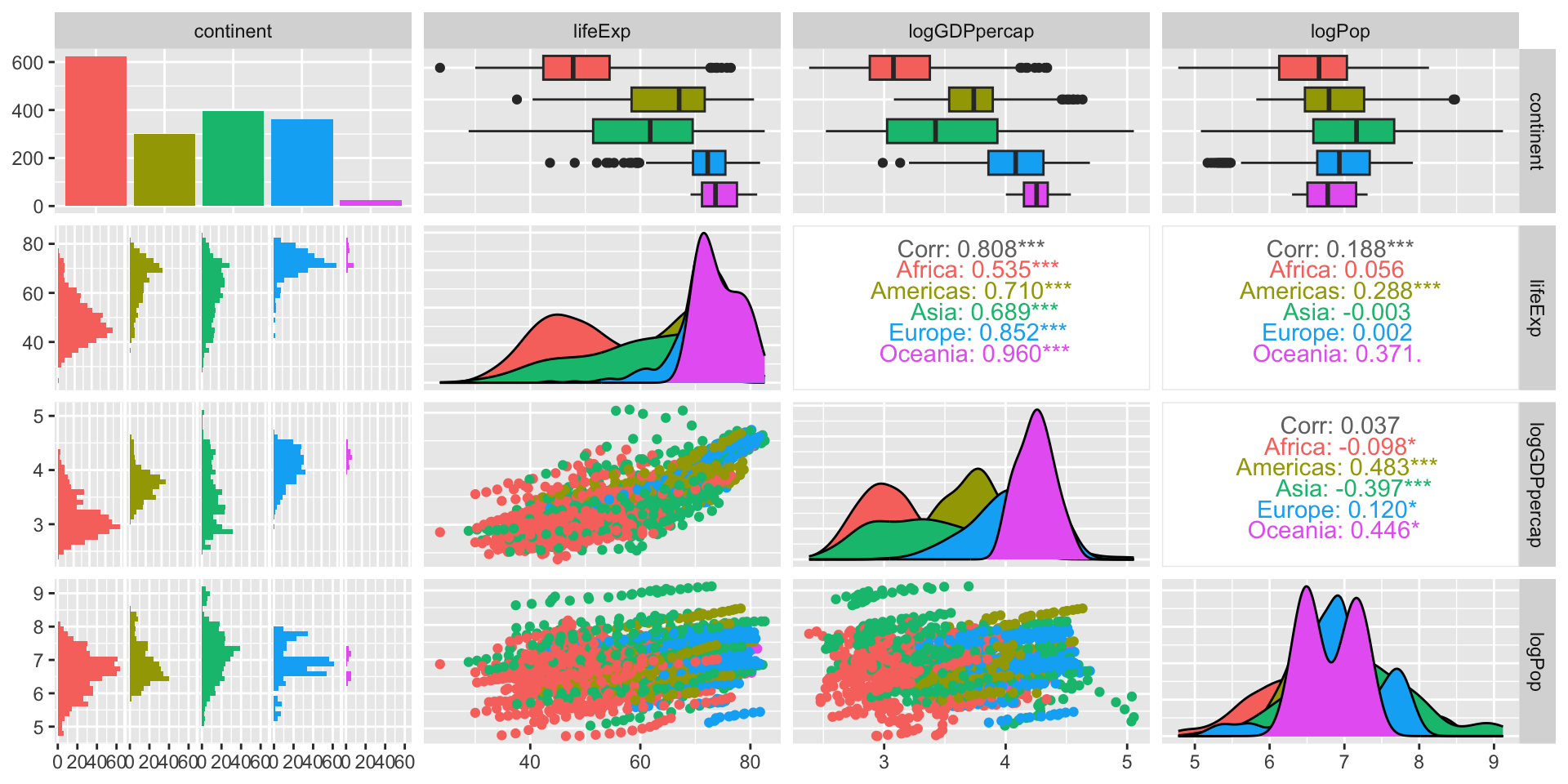
my_gapminder |> select(-year) |> ggpairs(aes(color = continent))

ggpairs is in the GGally package.

PCA: 2007 data only

pca1 <- prcomp(my_gapminder2 %>% select(-continent), scale=TRUE)
autoplot(pca1, data = my_gapminder2, loadings=TRUE, loadings.label = TRUE,
         colour = 'continent')

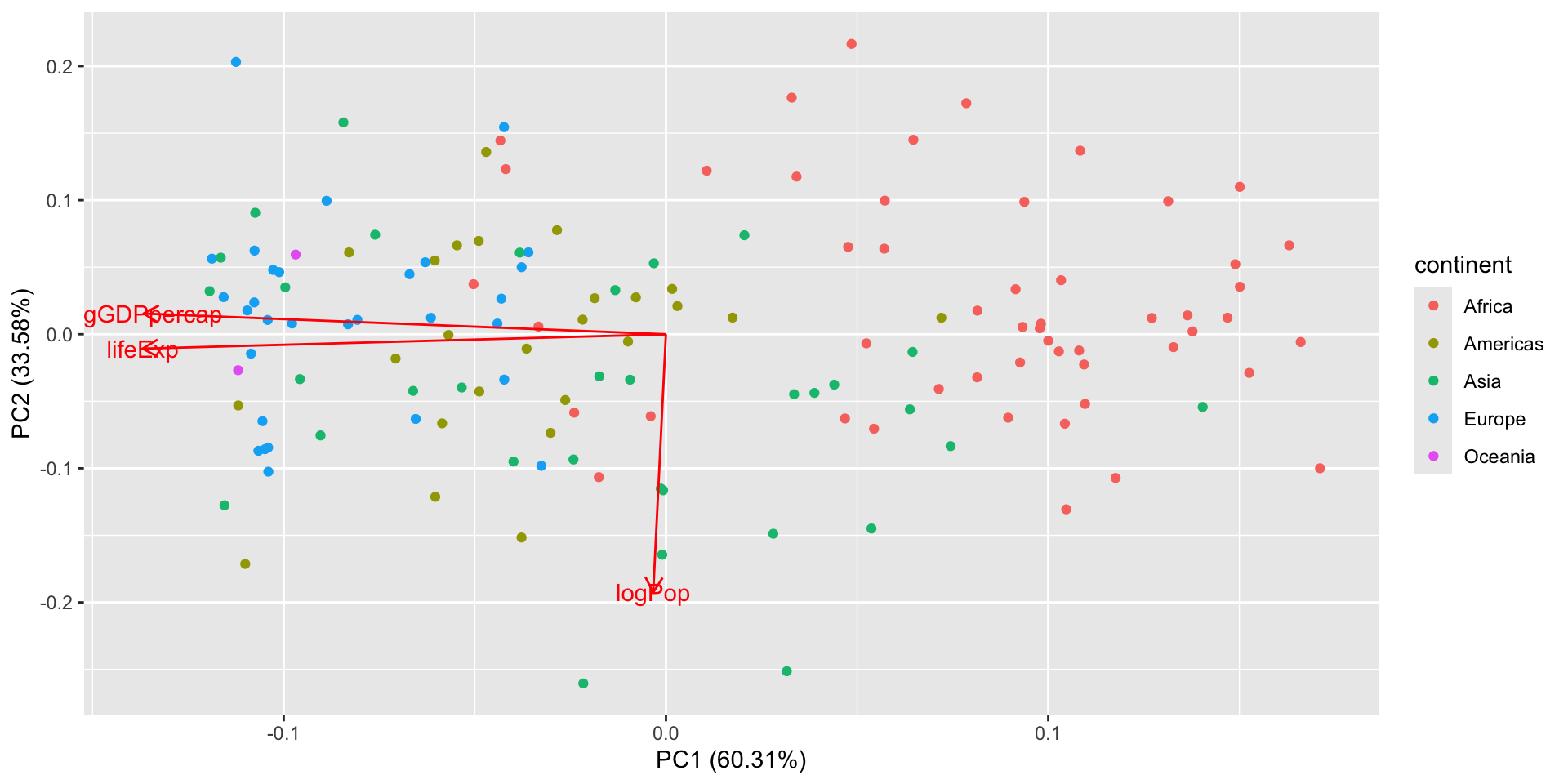
Loadings

This matrix tells you how to rotate the data into PC coordinates which is the weight of each original variable in the computation of PCs.

tidy(pca1, matrix = "rotation") |>
  pivot_wider(names_from = column, values_from = value) |> kable() |> kable_styling(full_width = FALSE)
PC lifeExp logGDPpercap logPop
1 -0.7075921 -0.7064117 -0.0172002
2 -0.0555353 0.0798613 -0.9952578
3 0.7044354 -0.7032813 -0.0957400

PCA: All years

pca1 <- prcomp(my_gapminder |> select(-continent, -year), 
               scale=TRUE)
autoplot(pca1, data = my_gapminder, loadings=TRUE, 
         loadings.label = TRUE, colour = 'continent')

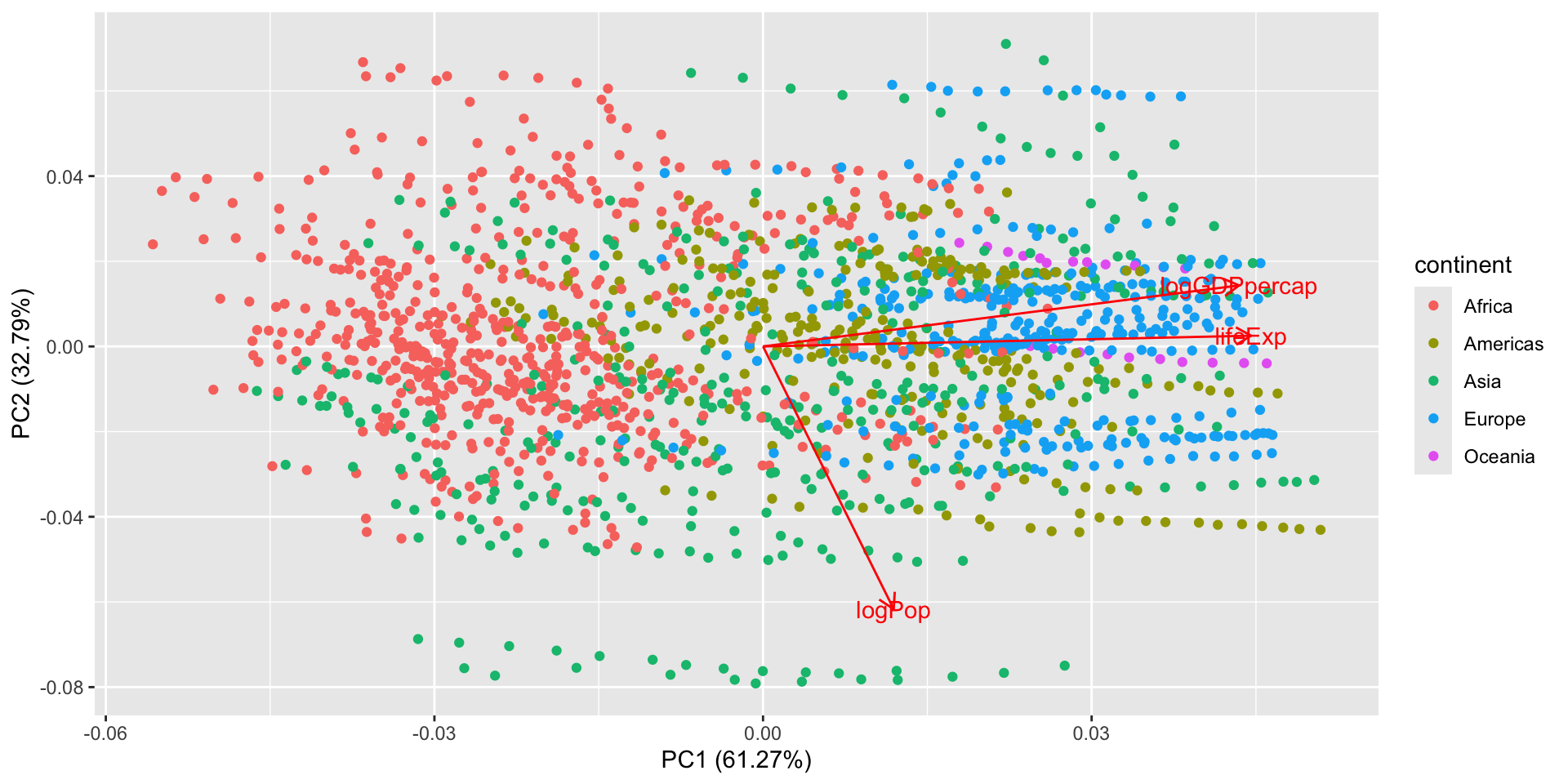
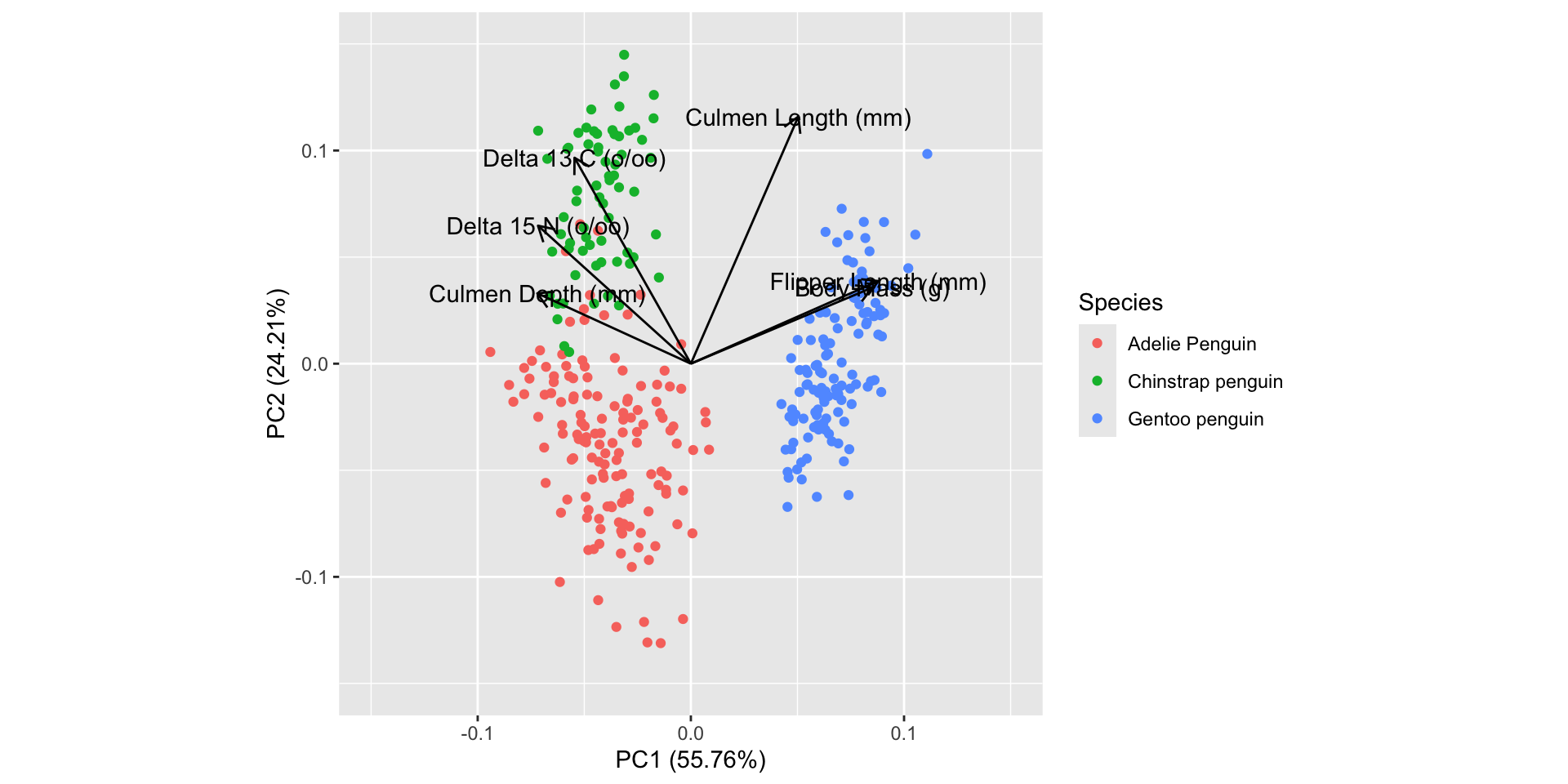
Penguins

pca2 %>% tidy(matrix="loadings") |> # same as rotation
  filter(PC < 3) |>
  pivot_wider(values_from="value", 
              names_from="PC", names_prefix="PC_") |> kable() |> kable_styling(full_width = FALSE)
column PC_1 PC_2
Culmen Length (mm) 0.2871721 0.6602934
Culmen Depth (mm) -0.4102740 0.1879624
Flipper Length (mm) 0.5008652 0.2207240
Body Mass (g) 0.4846484 0.2033560
Delta 15 N (o/oo) -0.4084370 0.3686830
Delta 13 C (o/oo) -0.3108644 0.5501663

Summary

  • Use PCA to reduce the number of dimensions (variables) in your data

  • Interpret loadings (arrows and numeric vectors)

  • Pay attention to the proportion of variance along each principal component

  • Consequences of scaling variables (or not scaling them)

Task

  • Bonus task: Practice the PCA skills in this lesson

Penguin PCA code

See the course notes for more code examples.

my_penguins_raw = penguins_raw |> select(-`Sample Number`) |>
  select(Species, where(is.numeric) ) |> na.omit() |>
  mutate(Species = str_remove(Species, "\\(.*\\)"))
pca2 <- my_penguins_raw |> select(-Species) |> prcomp(scale=TRUE)
autoplot(pca2, data = my_penguins_raw, 
         loadings=TRUE, loadings.label = TRUE,
         loadings.label.colour = "black", loadings.colour = "black",
         colour = 'Species') + xlim(-0.15, 0.15) + ylim(-0.15, 0.15)